Einfärben von Bildern - Zwei Ansätze
von Simon Drasch, Florian Eder & Moritz Enderle
Abstract
In der heutigen Zeit, in welcher große Mengen an Bildern leicht zugänglich sind, gewinnen die Nutzung und Verarbeitung dieser Daten mit Hilfe von KI an Bedeutung. Wir stellen zwei Methoden vor um das zu erreichen, pix2pix und Deoldify. Wir gliedern unsere Arbeit in drei Bereiche: Podcast, Präsentation mit Code-Demonstration und dieser schriftlichen Ausarbeitung.
In unserem Podcast bieten wir einen oberflächlichen Überblick über die verschiedenen Methoden und Anwendungsgebiete der Bildkolorierung. Dabei erklären wir die Mechaniken so einfach und verständlich wie möglich, um auch Zuhörer ohne Vorkenntnisse im Bereich der künstlichen Intelligenz anzusprechen.
In der Präsentation bieten wir tiefgehende Einblicke in den Aufbau und die Merkmale von Bildern. Zuerst stellen wir statistische Ansätze wie den Mean StD Transfer und Lab Mean Transfer kurz vor. Darüber hinaus gehen wir intensiv auf die KI-Systeme Pix2pix und DeOldify ein. Dabei werden die mathematischen Grundlagen hinter den Algorithmen erklärt. Der Fachvortrag richtet sich an ein Fachpublikum mit fortgeschrittenen Kenntnissen im Bereich der künstlichen Intelligenz und liefert detaillierte Informationen über die verschiedenen Ansätze zur Bildkolorierung.
Anschließend wird in der Code Demonstration anhand eines Beispieldatensatzes gezeigt, wie verschiedene Methoden zur Bildkolorierung angewendet werden Dabei wird der Einsatz von Pix2pix und DeOldify demonstriert, die Qualität der Ergebnisse miteinander verglichen und anschließend eine Einschätzung der Effektivität und Genauigkeit der verschiedenen Ansätze dargestellt.
Motivation
Unter Bildkolorierung versteht man die Methode, Schwarz-Weiß-Bildern Farben hinzuzufügen. Dadurch kann man ihnen neues Leben einzuhauchen und alte Bilder vollautomatisch und realistisch restaurieren. Sie ermöglicht es uns, visuelle Informationen und Details zu erfassen, die in Schwarz-Weiß-Bildern verborgen sind, vorallem da die Einbeziehung von Farben die Art und Weise, wie wir Bilder wahrnehmen und interpretieren, erheblich verändert. Das Hinzufügen von Farbe auf Schwarz-Weiß-Bildern ermöglicht somit eine Vielzahl von Anwendungen, von der Restaurierung alter Fotografien bis hin zur Verbesserung der visuellen Datenanalyse.
Ein Beispiel für den Einsatz von KI-Systemen in der Bildrestaurierung ist die Website Myheritage, welche Ahnenforschung, Stammbaumerstellung und genetische Genealogie betreibt. Darüber hinaus bieten sie zusätzlich an, alte Familienbilder einzufärben und diese mit anderen zu teilen, damit die Familiengeschichte nicht in Vergessenheit gerät.
Herausforderungen bei der Bildkolorierung liegen vor allem in der genauen Reproduktion von Farben und der Beibehaltung des ursprünglichen Bildcharakters. Neben technische Fähigkeiten muss auch ästhetisches Verständnis vorhanden sein, um qualitativ hochwertige Ergebnisse garantieren zu können.
Um solche Ergebnisse selbst erzeugen zu können, werden in den folgenden Abschnitten verschiedene Ansätze zur Bildkolorierung vorgestellt, darunter sowohl klassische Methoden als auch moderne KI-Systeme.
Methoden
In der Bildkolorierung werden verschiedene Methoden eingesetzt, die auf statistischen Ansätzen und KI-Systemen basieren.
Statistische Ansätze
Statistische Ansätze zur Bildkolorierung verwenden mathematische Modelle, um Farben zu Schwarz-Weiß-Bildern hinzuzufügen. Einfärben mit Hilfe von statistischen Modellen ist nicht möglich, jedoch wird die Farbübertragung eines Referenzbildes auf ein Schwarz-Weiß-Bild oft mit Einfärben betitlelt. Drei solcher statistischen Methoden sind:
- Mean StD Transfer: In dieser Methode wird das Helligkeits-und Farbniveau des Referenzbildes auf eine normalisierte Version des Schwarz-Weiß-Bildes übertragen. Dies wird mit der folgenden mathematischen Formel erreicht:
-
Dieser Ansatz ist zwar schnell und funktioniert einigermaßen okay, wenn man farbige Bilder umfärben möchte, jedoch wird bei Schwarz-Weiß-Bildern nur die Durchschnittsfarbe des Referenzbildes projeziert.
-
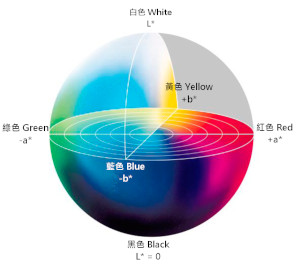
Lab Mean Transfer: Diese Methode funktioniert gleich wie der Mean StD Transfer, allerdings wird zuvor der Farbraum von RGB in Lab übertragen. Dadurch werden schon etwas bessere Ergebnisse erzeugt, allerdings sind auch diese bei Schwarz-Weiß-Bildern genau so schlecht.
-
Probability Density Function (PDF) Transfer: In diesem komplexen mathematischen Verfahren werden für beide Bilder ein normalisiertes Histrogramm erstellt, welche dann genutzt werden um die Wahrscheinlichkeitsverteilung von der Farbpalette des Schwarz-Weiß-Bildes (unterschiedliche Grautöne) auf die Farbpalette des Referenzbildes zu übertragen. Dieser Ansatz liefert die besten Ergebnisse der drei verschiedenen statistischen Ansätze, ist jedoch auch der komplexeste und rechenintensivste. Die Ergebnisse sind zwar besser als bei den anderen beiden Ansätzen, jedoch sind sie immer noch nicht zufriedenstellend.
Ergebnisse:
| Schwarz-Weiß-Bild | Referenzbild | Mean StD Transfer | Lab Mean Transfer | PDF Transfer |
|---|---|---|---|---|
 |
 |
 |
 |
 |
KI-Systeme
Conditional Adversarial Networks (cGAN)
Conditional Adversarial Networks (cGAN) sind eine Art von generativen Modellen, die auf dem Konzept der generativen adversariellen Netzwerke (GAN) basieren. GANs bestehen aus zwei neuronalen Netzen, die gegeneinander trainiert werden. Der Generator G versucht, Bilder zu erzeugen, die von einem menschlichen Betrachter nicht von echten Bildern unterschieden werden können. Der Diskriminator D versucht, die vom Generator erzeugten Bilder von echten Bildern zu unterscheiden. Sie teilen sich eine Lossfunktion, die den Generator dazu zwingt, bessere Bilder zu erzeugen, und den Diskriminator dazu zwingt, bessere Entscheidungen zu treffen. Sie sieht wie folgt aus:
Dabei hat der Generator die Aufgabe, den zweiten Teil der Lossfunktion zu minimieren, während der Diskriminator versucht, die vollständige Funktion zu maximieren.
Bei conditional Adversarial Networks wird der Generator und/oder Discriminator zusätzlich mit einem Konditionierungsterm erweitert. Dieser Term wird dem Generator als zusätzlicher Input übergeben und kann beispielsweise ein Label, ein Bild oder eine Zahl bzw Vektor sein. Dadurch kann der Generator Bilder erzeugen, die zu einem bestimmten Label passen. Die Lossfunktion sieht dann wie folgt aus:
Hier die beiden Teile der Lossfunktion erklärt:
⟶ Der Erwartungswert des Diskriminators, dass ein echtes Bild mit Label y als solches klassifiziert wird: D(x|y) soll gegen 1 gehen.
⟶ Der Erwartungswert des Diskriminators, dass ein generiertes Bild mit Label y als solches klassifiziert wird: D(G(z)) soll gegen 0 gehen.
Man betrachtet also die Wahrscheinlichkeit, dass der Diskriminator ein echtes Bild mit dem Label y von einem generierten Bild mit dem Label y unterscheiden kann. Der Generator versucht, diese Wahrscheinlichkeit zu minimieren, während der Diskriminator versucht, sie zu maximieren. Darüber hinaus wird der Generator trainiert, Bilder abhängig von einem Label zu erzeugen, daher der Begriff conditional.
Convolutional Neural Networks (CNN)
CNNs sind darauf spezialisiert, matrixartige Topologien, wie zum Beispiel Bilder, zu verarbeiten. Sie bestehen hauptsächlich aus Convolutional Layern, die jeweils aus mehreren Convolutional Filtern bestehen. Diese Filter sind kleine Matrizen, die über das Bild geschoben werden und dabei jeweils einen Teil des Bildes betrachten. Die Werte der Filter werden dabei trainiert, um bestimmte Muster zu erkennen. Die Filter werden dann auf das gesamte Bild angewendet und erzeugen eine neue Matrix, die sogenannte Feature Map. Diese Feature Map enthält Informationen über die Muster, die der Filter erkannt hat. Die Feature Map wird dann an den nächsten Convolutional Layer weitergegeben, der wiederum neue Muster erkennt. Auf diese Weise können CNNs komplexe Muster erkennen und klassifizieren. Weiterhin sind Pooling Layer, welche die Feature Maps verkleinern und somit genauere Muster erkennen können, und Fully Connected Layer, welche die Feature Maps in einen Vektor umwandeln um sie z.B. für eine Klassifizierung zu nutzen.
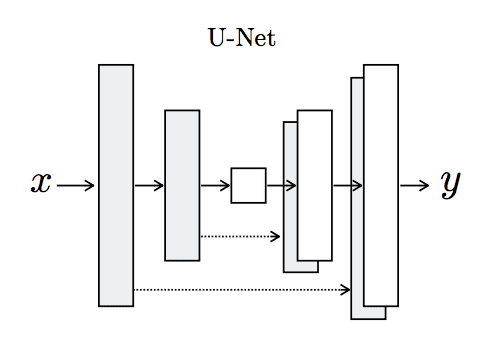
Das U-Net CNN ist ein Beispiel von CNNs, welches auf einem vortrainierten Residual Neural Network aufbaut. Der Input wird zuerst auf 256x256 Pixel reshaped und normalisiert. Danach wird das vortrainierte Residual Neural Network geladen und die ersten 18 Layer werden eingefroren. Die restlichen Layer werden dann durch Convolutional Layer ersetzt, die die Feature Maps erweitern. Die Feature Maps werden dann durch Upsampling Layer vergrößert und mit den Feature Maps der vorherigen Layer konkateniert. Dadurch werden die Feature Maps verfeinert und die Auflösung erhöht. Am Ende wird ein Convolutional Layer mit einem Filter der Größe 1x1 angewendet, um die Feature Maps auf die Anzahl der Klassen zu reduzieren. Die Feature Maps werden dann durch einen Softmax Layer klassifiziert.
Anwendungen
Pix2Pix
Das Pix2Pix Modell haben wir für die Code demo in PyTorch implementiert. PyTorch ist ein Open-Source-Deep-Learning-Framework, das von Facebook AI Research entwickelt wurde. Es bietet eine umfassende Plattform zur Entwicklung und Umsetzung von neuronalen Netzen in Python.
Das Pix2Pix Model basiert auf einem GAN Ansatz, wobei sowohl Generator als auch Diskriminator auf einer U-Net Struktur basieren. Ein U-Net ist ein tiefes neuronales Netzwerk mit einer U-förmigen Architektur. Es nutzt Skip Connections, um globale und lokale Informationen zu kombinieren und genaue Farbinformationen zu erzeugen. Diese werden durch Anhängen der letzten Conv2D Schicht des Encoders an die erste Conv2D Schicht des Decoders erzeugt. Dadurch soll der Diskriminator nicht nur Abnormalitäten erkennen, sondern auch die genaue Position der Abnormalität im Bild bestimmen können. Darüber hinaus basiert der Decoder auf dem PatchGAN Diskriminator, welcher das Bild in (hier: 70x70 Pixel) Patches aufteilt und für jedes Patch eine Wahrscheinlichkeit ausgibt, ob es sich um ein echtes oder generiertes Bild handelt. Dadurch erhält man schärfere Features und eine höhere Genauigkeit. Zudem hat diese Diskriminator Architektur weniger Parameter als ein normaler Diskriminator, was das Training beschleunigt.
In dieser cGAN Archtiktur bekommt nur der Diskriminator ein Label, das Schwarz-Weiß-Bild. Der Generator bekommt jediglich das Schwarz-Weiß-Bild als Input und soll ein Bild erzeugen, das zu diesem passt.
Der Diskriminator wird sowohl mit dem generierten Bild als auch mit dem Originalbild getestet, um zu sehen, wie gut er die beiden unterscheiden kann. Dabei wird der Binary Cross Entropy Loss verwendet. Dieser ist definiert als:
N ist in unserem Beispiel die Anzahl der Pixel im Bild. x ist der Output des Diskriminators, y ist die tatsächliche Wahrheit. 0 steht für ein generiertes Bild, 1 für ein echtes Bild. Der Loss wird dann für beide Bilder berechnet und anschließend der Durchschnitt gebildet.
Der Generator wird mit dem generierten Bild getestet. Dabei wird der L1 Loss verwendet. Dieser ist definiert als:
N ist in unserem Beispiel die Anzahl der Pixel im Bild. x ist der Output des Diskriminators, y ist das Originalbild. Zusätzlich wird der geupdatete Diskriminator verwendet, um zu sehen, wie gut der Generator die beiden Bilder unterscheiden kann. Dabei wird der Binary Cross Entropy Loss mit folgenden Einstellungen verwendet:
- x ist der Output des Diskriminators auf Fake Bild mit Schwarz-Weiß-Bild als Label
- y ist das Originalbild Dadurch sagt die Lossfunktion aus, wie sehr der Diskrimator glaubt, dass das generierte Bild zu dem Schwarz-Weiß-Bild nicht passt.

Zum Trainieren des Modells haben wir den COCO-Datensatz verwendet, der 123.287 Bilder enthält. Aufgrund unserer begrenzten Trainingsressourcen haben wir nur 10k zufällig ausgewählte Bilder verwendet.
Die Bilder wurden auf 256x256 Pixel skaliert und in den Lab-Farbraum konvertiert. Der L-Kanal wurde als Eingabe für den Generator und die Ab-Kanäle als Ziel verwendet. Der Diskriminator wurde mit dem L-Kanal des Eingangsbildes und den Ab-Kanälen des Zielbildes trainiert.
Das Modell wurde für 70 Epochen mit einer Stapelgröße von 32 trainiert. Die Verlustfunktion war eine Kombination aus dem L1-Verlust und dem kontradiktorischen Verlust. Der L1-Verlust ist ein einfacher mittlerer absoluter Fehler zwischen dem vorhergesagten und dem Zielbild. Der gegnerische Verlust ist der binäre Kreuzentropieverlust zwischen dem vorhergesagten und dem Zielbild. Der adversarial loss wird zum Trainieren des Diskriminators und des Generators verwendet. Der L1-Verlust wird nur für das Training des Generators verwendet.
Zum optimieren des Modells brauchen wie die jeweilige Backward Funktion für den Generator und den Diskriminator:
def backward_D(self):
"""
Backward pass for the discriminator.
"""
fake_image = torch.cat([self.L, self.fake_color], dim=1)
fake_preds = self.net_D(fake_image.detach())
self.loss_D_fake = self.GANcriterion(fake_preds, False)
real_image = torch.cat([self.L, self.ab], dim=1)
real_preds = self.net_D(real_image)
self.loss_D_real = self.GANcriterion(real_preds, True)
self.loss_D = (self.loss_D_fake + self.loss_D_real) * 0.5
self.loss_D.backward()
def backward_G(self):
"""
Backward pass for the generator.
"""
fake_image = torch.cat([self.L, self.fake_color], dim=1)
fake_preds = self.net_D(fake_image)
self.loss_G_GAN = self.GANcriterion(fake_preds, True)
self.loss_G_L1 = self.L1criterion(self.fake_color, self.ab) * self.lambda_L1
self.loss_G = self.loss_G_GAN + self.loss_G_L1
self.loss_G.backward()
Während des Training Vorgangs werden nun diese beiden Funktionen hergenommen um in der optimize() Funktion die Gewichte zu trainieren:
def optimize(self):
"""
Optimize the model.
"""
self.forward()
self.net_D.train()
self.set_requires_grad(self.net_D, True)
self.opt_D.zero_grad()
self.backward_D()
self.opt_D.step()
self.net_G.train()
self.set_requires_grad(self.net_D, False)
self.opt_G.zero_grad()
self.backward_G()
self.opt_G.step()
Um das trainierte Modell für eine Prediction zu nutzen, können wir Bilder in den L-Space konvertieren und den Generator nutzen um eine Farbvorhersage zu treffen:
batch_prp = preprocess(batch)
fake_imgs = predict(model, batch_prp)
fake_imgs = [Image.fromarray((img * 255).astype(np.uint8)) for img in fake_imgs]
Da unser Modell nur sehr begrenzt trainiert wurde, sind die Ergebnisse nicht mit dem aktuellen Stand der Technik vergleichbar. Dennoch sind die Ergebnisse für ein so einfaches Modell sehr gut.

DeOldify
DeOldify ist im Gegensatz zu unserem selbst-trainierten Modell ein bereits kommerziell etablierted Modell und bietet daher auch schon vortrainierte Gewichte an. Diese können wir nutzen um unsere Bilder zu färben.
Was DeOldify besonders macht ist unter Anderem der NoGAN Ansatz. Das bedeutet in diesem Fall, dass wir Generator und Diskriminator seperat voneinander trainieren und erst nachdem beide vollständig trainiert wurden, zusammenführen. Der Diskriminator wird dabei nur für das Training des Generators verwendet und überträgt sein Wissen sehr schnell an den Generator.
Die Lossfunktion des Models besteht aus zwei Teilen, den Farbloss und dem Kontentloss. Beim Farbloss wird der L1-Unterschied zwischen den RGB-Werten des Originalbildes und des gefärbten Bildes berechnet. Das Kontentloss ist ein Featureloss, das die Unterschiede zwischen den Featuremaps des VGG16-Netzwerks berechnet.
Möchte man das ganze selber ausprobieren, muss man folgenden Code ausführen:
for image in images_real_bw:
deoldify_colorized.append(
colorizer.filter.filter(
image, image, render_factor=35, post_process=True
)
)


Eine Stärke, die sich durch den NoGAN Ansatz herauskristallisiert, ist die Fähigkeit, Videos einzufärben. Diese sind deutlich Farbintensiver und beinhalten weniger Farbflickern als mit herkömmlichen GANs.

Fazit
Die Bildkolorierung ist ein aktives Forschungsgebiet, das sowohl statistische Ansätze als auch KI-Systeme umfasst. Statistische Methoden wie der Mean StD Transfer und der Lab Mean Transfer bieten schnelle und effiziente Lösungen, haben aber ihre Grenzen, insbesondere bei der Verarbeitung von Schwarz-Weiß-Bildern. Auf der anderen Seite bieten KI-Systeme wie Pix2pix und DeOldify neue Möglichkeiten zur Verbesserung der Bildkolorierung. Diese Systeme verwenden lernfähige Modelle, die sich an verschiedene Arten von Bildern anpassen können, und bieten daher das Potenzial für verbesserte Genauigkeit und Vielseitigkeit. Trotz der Fortschritte in diesem Bereich gibt es immer noch Herausforderungen und Raum für Verbesserungen.
Materialien
Podcast
Der Campus Talk – Silicon Forest – Folge 5
Talk
Hier einfach Youtube oder THD System embedden.
Demo
Link zum Repository: https://mygit.th-deg.de/me04536/recolor
Literaturliste
Autoren
- Florian Eder
- Moritz Enderle
- Simon Drasch